今回は走査型電子顕微鏡(SEM)や電子プローブマイクロアナライザー(EPMA:Electron Probe Micro Analyzer)を用いて、試料にどの様な元素が含まれているのかを分析する手法を紹介します。どちらの装置も電子線を試料に照射し、試料から帰ってきた信号を解析することで試料由来の情報を得ることができます。もちろんSEMは元素分析をするための装置ではありませんので、分析装置を取り付けることで試料の分析ができるようにします。
元素分析の原理
試料中にどのような物質(元素)が含まれているかを調べる手法の一つに特性X線を使う手法があります。SEM、EPMAでは、この特性X線を使うことで試料中の元素を判別しています。原子は外部からのエネルギーによって励起された電子が元の軌道に戻る際や、電子が抜けた軌道により高い軌道の電子が遷移してくるときに特定の波長の電磁波を放出する性質を持っています。
外部から与えられたエネルギーをhν、放出されるエネルギーをhν'とすると、次の図の様になっています。
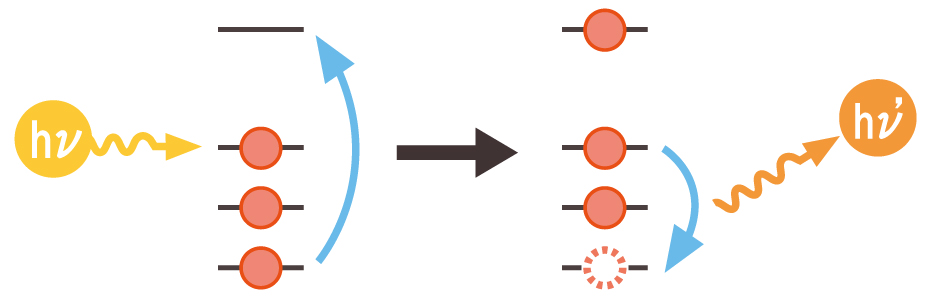
図:特性X線放出のメカニズム
この放出される電磁波の波長は主にX線領域です。SEMやEPMAによって試料に電子線を当てることで、出てくるX線スペクトルがどの波長で輝線を示すかによって、試料に含まれる元素を判別できます。
原子の構造を交えて、もう少し詳しく説明しましょう。高校の物理で学習したとおり、原子は原子核と電子から成り立っています。そして電子の軌道は内側からK殻、L殻、M殻、N殻・・・と名付けられており、元素とその状態によってどの軌道まで電子が埋まっているのかが変わります。例えば鉄原子は原子番号が26ですので、N殻までを含めて26個の電子が存在しています。
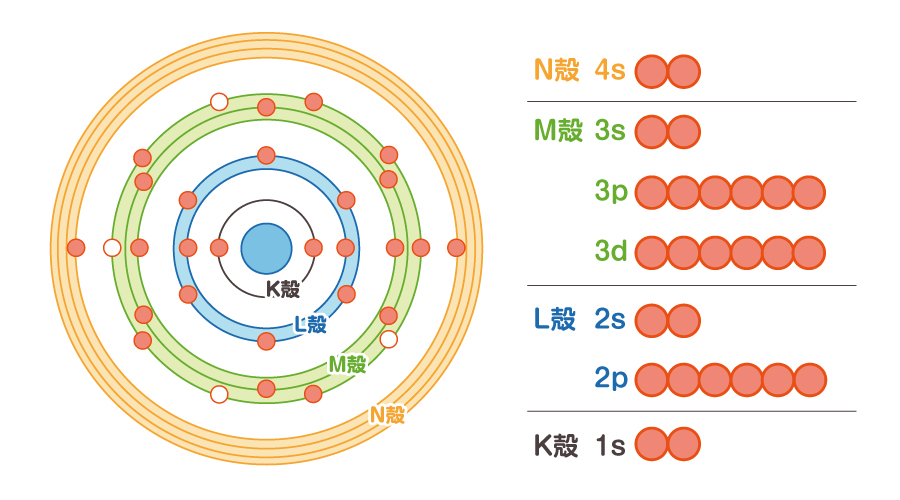
図:鉄原子の電子軌道模式図
さて、原子に含まれる電子は外部から強いエネルギーを与えられると、本来の軌道から飛び出してしまいます。これを励起と言います。外側の軌道と比較して、内側の軌道から電子を励起させる方が、より強いエネルギーが必要です。一方、電子が励起し飛び出したことによって空いた場所には、より高い軌道から電子が降りてきます。この時、高い軌道と、遷移した場所の低い軌道の差のエネルギーを電磁波の形で放出します。どの軌道から、どの軌道への遷移であるかによって、Kα線、Kβ線、Lα線、Lβ線など、名称が決められています。
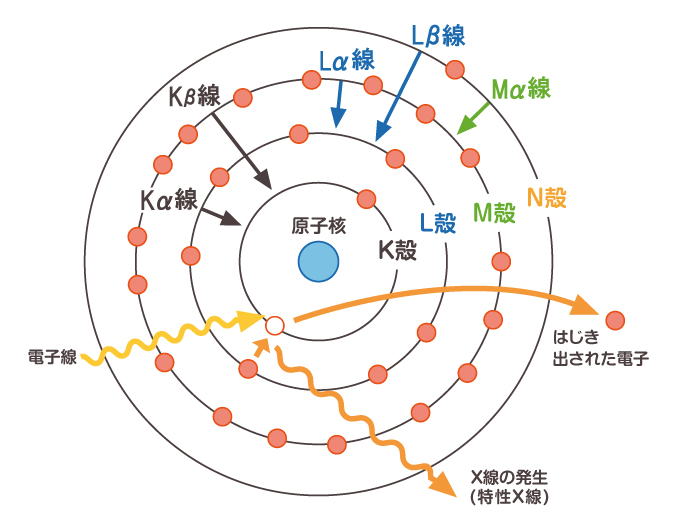
図:電子軌道と特性X線の発生
そして放出される電磁波のエネルギーは、どの元素の何番目の軌道から遷移したものかによって、ユニークに決まっています。L殻からK殻へ電子が遷移する際に放出されるエネルギー(Kα線)を例に取ると、これは元素ごとに固有のエネルギー値を持っています。そのため放出される電磁波の波長も決まっているのです。このX線を特性X線と呼びます。ちなみに電子の励起にX線を利用した場合には、発生する特性X線のことを「蛍光X線」と呼びます。
つまりSEMやEPMAで試料に電子線を照射すると、試料中に含まれる原子の電子が励起し、空いた場所に高い軌道から電子が遷移して、元素に応じたX線を放出します。このX線を観察・解析することによって、試料に含まれる元素固有の情報を得ることができます。
特性X線を分析する手法は大きく分けて二つあります。一つ目は「波長分散型X線分析(WDS:Wavelength-dispersive X-ray spectroscopy)」と呼ばれ、分光結晶を用い特性X線を分光し、波長分解された波長を検出します。
二つ目は「エネルギー分散型X線分析(EDS:Energy-dispersive X-ray spectroscopy)」と呼ばれ、半導体検出器を用いることで、特性X線をエネルギーごとに検出しています。どちらの手法もSEM、EPMAともに利用されています
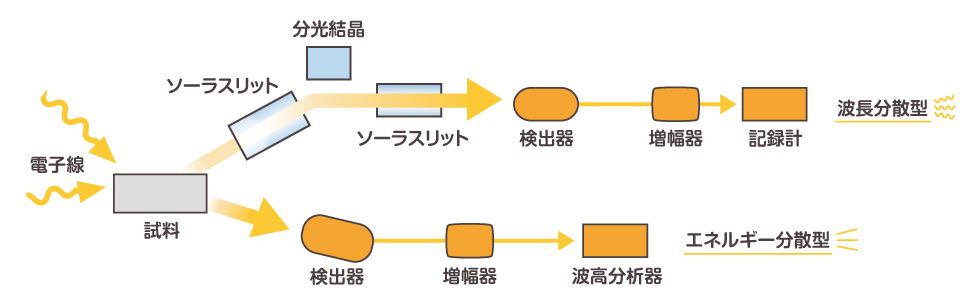
図:波長分散型とエネルギー分散型
2種類の元素分析方法があるわけですが、もちろんそれぞれに長所と短所があります。WDSはエネルギー分解能(波長分解能)が10eV程度と高分解能を持ち、散乱X線などの影響が少なくバックグラウンドノイズが小さいという長所を持っています。また数ppm程度の微量分析が可能です。その反面、一度に測定できる波長領域が狭く、分光結晶を測定波長によって切り替えるという機械的制御が必要なため、一度に複数の元素を特定することはできません。また、分光結晶による波長の分光も精度の高い制御が必要とされ、装置も大型になりがちです。これら、装置の大型化、測定の長時間化といったことがデメリットとして挙げられます。
一方EDSは一つの半導体で検出し、測定に必要な稼働部品も少ないため、小型で短時間での計測が可能です。さらに一度に多くの元素を調べられるのも長所です。しかし、近年では性能も上がってきているとは言え、エネルギー分解能は130eV(MnのKα線の場合)程度しかなく、バックグラウンドノイズも大きくなりがちです。また、最低でも10~20ppm以上含まれていなければ検出ができません。ですから使い分けが必要となります。
ちなみに装置が小型で済むEDSはSEMで主に使われます。一方、WDSは電子線のエネルギー装置が大型化することもありEPMAで利用されます。もちろんEDSをEPMAで利用することも可能です。EPMAはSEMと比較すると、元素の分析を主体にしたものといえます。
では実際に得られたスペクトルを見てみましょう。下の図は酸化鉄をEDSによって分析した結果得られたスペクトルです。横軸は波長をエネルギー(キロエレクトロンボルト)で表し、縦軸は検出されたフォトンの個数(カウント数)を示しています。
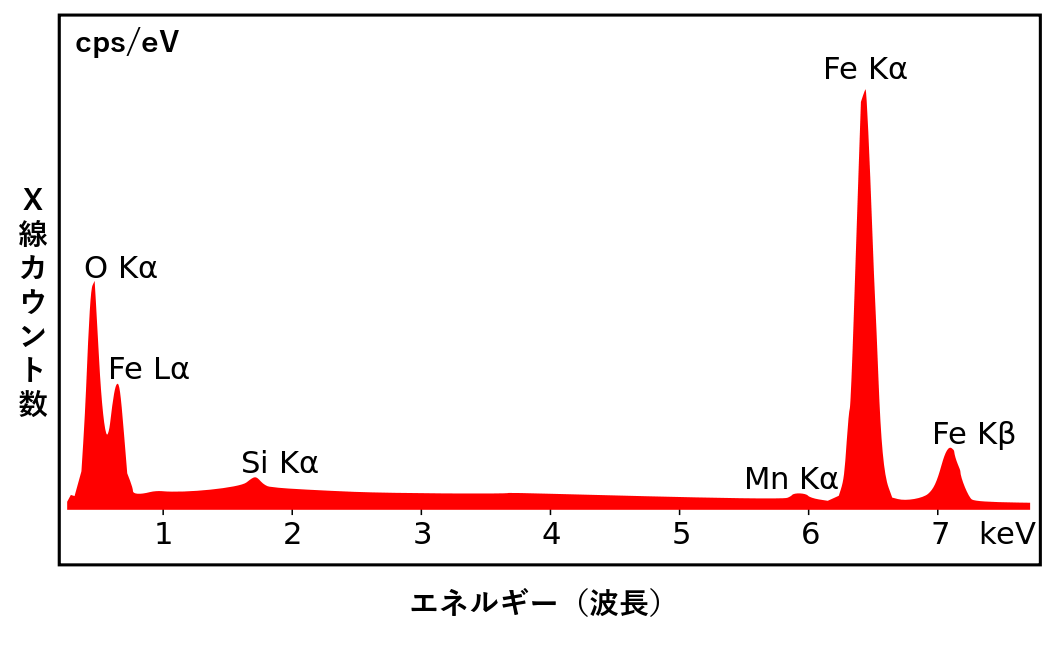
図:酸化鉄のEDSスペクトル(© Rainer Ziel:CC BY 3.0)
このスペクトルでは鉄(Fe)のKα線、Kβ線、Lα線が見えています。また酸素(O)のKα線が出ているのがわかります。鉄と酸素では同じKα線でエネルギー(波長)が異なるのがわかります。そしてピークの高さ(正確には面積)は元素の濃度を示していると考えて構いません。ですから、スペクトルから物質中に鉄と酸素が多いことがわかり、もしこの試料が未知試料だった場合、酸化鉄であるという結論が導き出せます。
またこの試料には不純物としてマンガン(Mn)とケイ素(Si)が微量ながら含まれていることもわかります。このように、不純物がどの程度混入しているのかを特定することも可能です。
他の分析方法
SEMやEPMAで電子線を試料に照射した際、特性X線以外にも発せられるものがあります。一つは電子で、これには反射電子と二次電子、オージェ電子があります。もう一つは、可視光領域で発せられる電磁波です。
では、SEMやEPMAを利用した他の分析方法を2つ紹介しましょう。
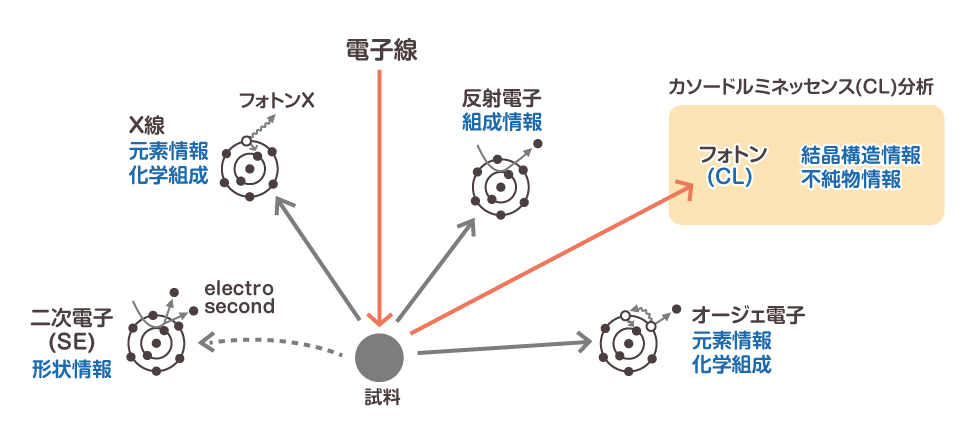
図:電子線照射時に発せられるもの
カソードルミネッセンス(CL:Cathode Luminescence)
この方法は、電子線を試料に当てた際に発せられる可視光線を利用します。この発光を「カソードルミネッセンス」と呼びます。そしてこの発光のスペクトルを利用して試料の物性を評価する方法を「カソードルミネッセンス法」といいます。
SEMを用いたカソードルミネッセンス法の場合、電子線によってもたらされる他の信号(二次電子、反射電子、X線など)も同時に取得できるため、複合的に物性の評価ができるという特徴を持っています。
カソードルミネッセンス法では、試料の結晶構造や、不純物の濃度を調べることができます。対象としては半導体や誘導体・セラミックスが中心で、結晶構造の欠陥などの材料解析などに使われます。また、酸化物や誘導体材料の不純物測定にも用いられます。

図:InGaN crystalのCL疑似カラー画像
(©FDominec:CC BY 4.0)
電子線後方散乱回折(EBSD:Electron Back Scattered Diffraction Pattern)
この方法は、試料表面で回折を受けた反射電子を利用します。これによって結晶の方位を解析します。 試料を電子線の入射角に対して60~70度傾斜させると、試料の結晶構造に影響を受け、結晶面での回折によって菊池線と呼ばれる白線と黒線が複数発生した菊池図形(または菊池パターン)が発生します。

図:菊池パターン(© P. Fraundorf:CC BY 4.0)
このパターンから、試料表面で結晶面がどの方位になっているかを知ることができます。つまり微小領域の結晶方位同定と方位マップの測定に使用できるわけです。もし、一様な結晶構造にならず、複数の微小結晶が結合しているような構造の場合、結晶方位が場所によって変わってしまうため、菊池線の方向も変化します。このパターンから、結晶の様子をマッピングすることができるのです。

図:結晶方位マップの例(Public Domain)
関連コラム
関連製品
松定プレシジョンでは、独自の高画質走査電子顕微鏡を製造販売しています。
参考文献
- 一般社団法人日本分析機器工業会 「X線分析法の基礎と応用」
https://www.jaima.or.jp/jp/analytical/basic/xray/foundation - 大阪産業技術研究所 「設備機器技術講習会[エネルギー分散型X線分析装置]」
http://tri-osaka.jp/c/content/files/archives/EDX200503.pdf - EBSP法の基礎原理と活用法(I)
https://www.jstage.jst.go.jp/article/kenbikyo2004/39/2/39_2_121/_pdf - 鳥取大学技術部 工学・情報系部門 「EPMAのしくみと試料分析例」
http://www.eng.tottori-u.ac.jp/~www_tec/epma/epma.html - 室蘭工業大学 「EPMAについて」
https://www.muroran-it.ac.jp/mat/momo/intro/epma/epma.html - 京都大学 「菊池線解析について」
http://www.tsujilab.mtl.kyoto-u.ac.jp/01TsujiLab/Education/AdvMaterDesign/2008/TextByTerada.pdf



 0120-747-636
0120-747-636


